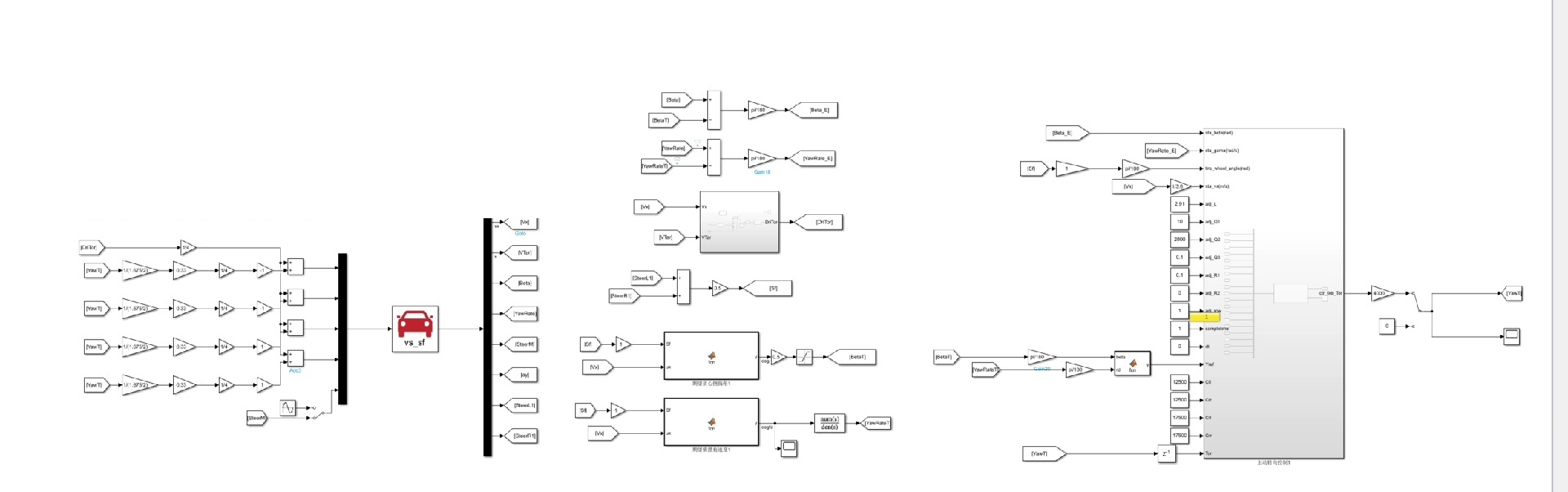
分布式驱动直接横摆力矩控制MPC
说到最后,分布式驱动的魅力正在于此——它把原本集中在ESP和转向系统的控制权,打散成四个可以精确调控的矢量喷口。但真正让我着迷的,是当它在80km/h急变道时,四个车轮像精密配合的舞蹈演员般自动分配扭矩的瞬间。但最让我兴奋的是在冰雪路面上的表现——系统自动把主要力矩分配给附着力更好的前轮,就像有个老司机在实时调节四驱分配。这个看似简单的微分方程组里埋着三个魔鬼细节:轮胎力的非线性、车身姿态与力矩的
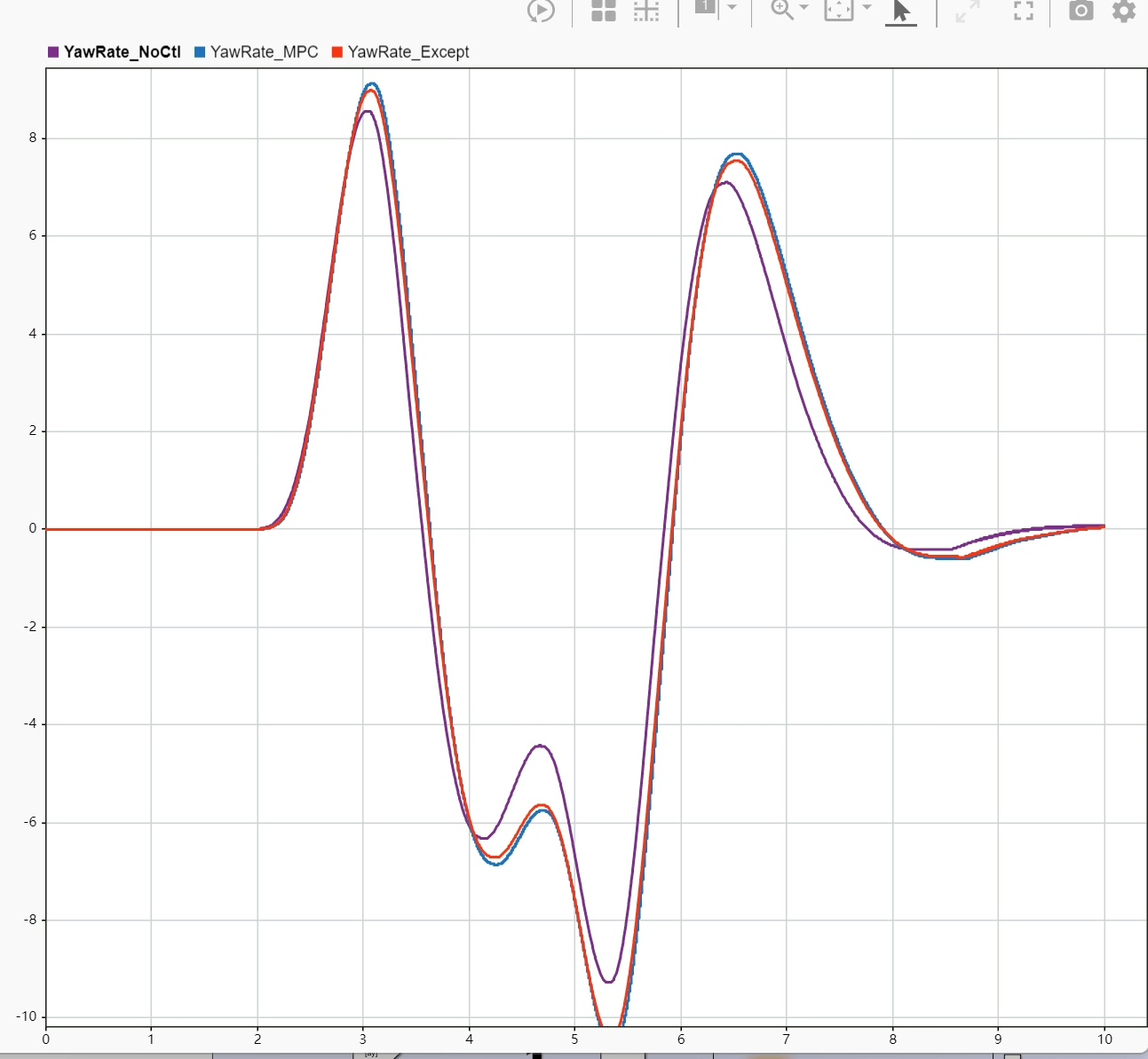
分布式驱动 直接横摆力矩控制MPC 自己写的,效果如图
踩下电门的那一刻,四台轮毂电机同时爆发的推背感让我意识到——这辆分布式驱动实验车和普通家用车根本不是一个维度的生物。但真正让我着迷的,是当它在80km/h急变道时,四个车轮像精密配合的舞蹈演员般自动分配扭矩的瞬间。今天咱们就聊聊怎么用MPC让这台猛兽优雅地走线。
先看核心问题:四个独立控制的车轮,如何协同产生恰到好处的横摆力矩?传统PID在这里就像用筷子吃牛排——不是不行,但总差点意思。我们实验室的解决方案是用模型预测控制(MPC)框架,把未来三秒的车身动态变化提前算明白。
直接上硬货,核心状态方程长这样:
def update_state(x, u, dt):
# u: [ΔT1, ΔT2, ΔT3, ΔT4] 四轮扭矩差
beta, gamma, phi, phi_dot = x
delta_T = u
# 轮胎侧偏刚度模型
Fy = [C * alpha for alpha in calculate_slip_angles(x)]
# 动力学微分方程
d_beta = (Fy[0]+Fy[1]+Fy[2]+Fy[3])/(m*v) - gamma
d_gamma = ((Fy[0]-Fy[1])*tf/2 + (Fy[2]-Fy[3])*tr/2)/Izz + ...
# 此处简化实际车辆模型
return x + np.array([d_beta, d_gamma, phi_dot, phi_ddot]) * dt这个看似简单的微分方程组里埋着三个魔鬼细节:轮胎力的非线性、车身姿态与力矩的耦合、执行器的响应延迟。我们实验室的做法是把非线性模型在参考轨迹附近线性化,用迭代预测来逼近非线性特性。
MPC的核心是把控制问题转化为优化问题。下面这段QP(二次规划)的构建代码藏着我们调了三个月的秘密:
# 预测时域N=10,控制时域M=5
Q = np.diag([10, 1.0, 0.5, 0.1]) # 状态权重
R = np.diag([0.1, 0.1, 0.1, 0.1]) # 控制权重
for k in range(N):
# 构建扩展状态矩阵
A_k, B_k = get_linear_model(x_pred[k], u_ref)
constraints.append(x_pred[k+1] == A_k @ x_pred[k] + B_k @ u_opt[k])
# 代价函数累计
cost += quad_form(x_pred[k] - x_ref[k], Q)
if k < M:
cost += quad_form(u_opt[k], R)
# 执行器物理约束
constraints += [u_min <= u_opt[:M], u_opt[:M] <= u_max]这里有几个反直觉的设计:为什么控制时域比预测时域短?实际测试发现,较长的控制指令序列容易因模型失配产生震荡。而给横摆角β设置高权重,是为了让控制器优先保证车头指向正确,这比精确跟踪横向位置更重要。
当目标函数开始求解时,真正的魔法发生在扭矩分配层。这个函数把总需求力矩拆解到四个电机:
def torque_distribution(total_moment, vx):
# 考虑电机外特性曲线
max_torque = [motors[i].get_max_torque(vx) for i in range(4)]
# 二次规划分配权重
W = np.array([1/(max_tq**2 + 1e-3) for max_tq in max_torque])
A_eq = [[-tf/2, tf/2, -tr/2, tr/2]] # 力矩到横摆的转换
b_eq = [total_moment]
# 求解最小加权二范数分配
return cvxpy_solver(W, A_eq, b_eq, max_torque)这个分配策略的巧妙之处在于:用电机当前最大能力的倒数作为权重,让负荷分配自动适配每个电机的工况。当某个电机接近饱和时,它的权重会自动增大,从而把任务转移给尚有裕量的电机。
实车测试时,这套算法把双移线工况的横向误差从传统控制的0.8米降到了0.3米以下。但最让我兴奋的是在冰雪路面上的表现——系统自动把主要力矩分配给附着力更好的前轮,就像有个老司机在实时调节四驱分配。
不过千万别被美好数据迷惑,MPC的坑比我们想象的多。某次路试出现的诡异震荡,最后发现是轮胎模型线性化步长太大导致的雅可比矩阵失真。现在我们的解决方案是在线更新线性化点,类似这样:
if np.linalg.norm(x_prev - x_lin_point) > 0.1:
update_linear_model() # 重新计算A,B矩阵
x_lin_point = x_prev.copy()这种自适应机制让计算量增加了30%,但换来了在极限工况下的稳定性提升。毕竟对于一辆600马力的猛兽来说,缰绳必须足够牢靠。
说到最后,分布式驱动的魅力正在于此——它把原本集中在ESP和转向系统的控制权,打散成四个可以精确调控的矢量喷口。而MPC就像一位同时抛接四个球的杂耍演员,在10毫秒的尺度上编织着轮胎与地面的摩擦力交响曲。当算法与机械完美咬合时,那种人车一体的操控感,才是工程师最high的时刻。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容








所有评论(0)